指数平滑移動平均線(EMA)の計算方法をどこよりも詳しく解説するよ!
もしかすると単純移動平均線(SMA)よりも、もっと多くの人に使われているかもしれない指数平滑移動平均線(EMA)。
今回は指数平滑移動平均線(EMA)の詳しい計算方法を解説します。
まずは概念から。
指数平滑移動平均線(EMA)は、より直近の価格データに比重を置いた移動平均線です。
そして今回の主役、EMA(指数平滑移動平均線)です。難しい言い回しをすれば「データの比重を指数関数的に減少させて算出」した移動平均線ということ。つまり、新しい日付の終値ほど比重を高めて平均値を出します。10EMAならば(日足の場合)、10日前の終値よりも1日前の終値の比重を大きくして計算するわけですね。古い終値よりも直近の終値を重視した移動平均線ということになります。
関連記事
単純移動平均線(SMA)と比べて、レートの動きに対してより敏感に反応するのが指数平滑移動平均線(EMA)です。
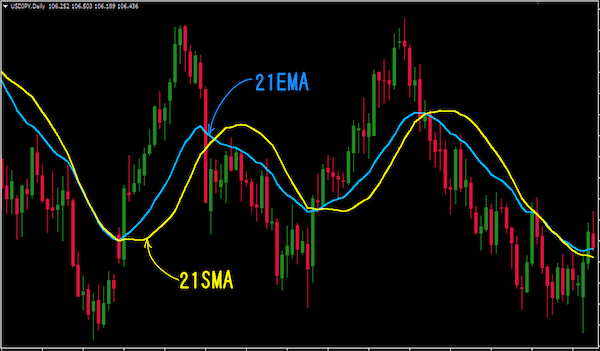
21SMAと21EMA
では具体的な計算方法を解説します。
指数平滑移動平均線(EMA)の計算方法は3段階
EMAは以下の3段階を経て計算をおこないます。
EMA計算の3ステップ
- SMAを計算する
- 比重をかけるための平滑化定数を計算する
- EMAを計算する
ステップ1|SMAを計算する
まずはSMA(単純移動平均線)を計算します。これはシンプルですね。「n」期間の終値の合計を「n」で割れば算出できます。
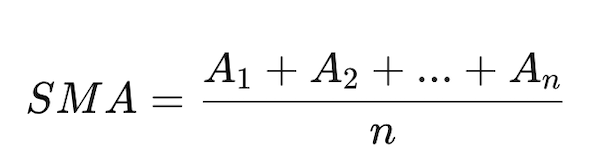
SMAを計算する
この数値が1日目の指数平滑移動平均線の値になります。
ステップ2|比重をかけるための平滑化定数を計算する
次に、2日目以降のEMAを算出するために、平滑化定数を計算します。
平滑化定数は、直近の価格データに比重をかけるための重要な要素です。
計算式は次の通り。
例えば期間「20」の移動平均線を計算する場合は次の通り。
この0.095(9.5%)が期間「20」における平滑化定数です。
平滑化定数によって価格データに対する比重の減少度合いを決定します。平滑化定数は後ほど詳しく解説します。ここではざっくりと「直近の価格にどれくらいの重みをかけるか?」という意味にとらえてください。
仮に期間「10」ならば…
0.18(18%)となります。
つまり短期EMA(例えば期間10)の方が長期EMA(例えば期間20)に比べて、直近の価格に対する加重が大きくなるわけです。
- 期間10 → 平滑化定数18%
- 期間20 → 平滑化定数9.5%
そのため、(長期EMAに比べて)短期EMAの方がより価格データ(=レート)に追従することになります。
ステップ3|EMAを計算する
さて、いよいよ2日目以降のEMAを計算します。EMAの計算式は以下の通り。
解説サイトによっては以下の計算式で解説しているケースもあります。
2つの式は異なりますが、どちらも同じ内容を計算しています(※どちらでも計算結果は同じ)。
【2026年1月版】優位性の高いFX商材 Best4
指数平滑移動平均線(EMA)を計算してみよう!
では先の計算式を使って、具体的な数値を使ってEMAを計算してみましょう。
ここでは、わかりやすく3日間の終値を使ったEMAを計算します。
使用するデータはこちら。
| 日 | 終値 |
| 1日 | 110円 |
| 2日 | 115円 |
| 3日 | 120円 |
| 4日 | 120円 |
| 5日 | 128円 |
| 6日 | 135円 |
ステップ1
まずは期間「3」の単純移動平均を算出します。過去3日間の終値が必要なので3日目から計算できますね。
| 日 | 終値 | EMA |
| 1日 | 110円 | |
| 2日 | 115円 | |
| 3日 | 120円 | (110+115+120)÷3=115 |
| 4日 | 125円 | |
| 5日 | 128円 | |
| 6日 | 135円 |
ステップ2
次に期間「3」の平滑化定数を算出します。
(2/(3+1))=0.5
平滑化定数は0.5です。
ステップ3
平滑化定数「0.5」を使って4日目以降のEMAを計算していきます。
| 日 | 終値 | EMA |
| 1日 | 110円 | |
| 2日 | 115円 | |
| 3日 | 120円 | (110+115+120)÷3=115 |
| 4日 | 125円 | (125−115)✕0.5+115=120 |
| 5日 | 128円 | (128−120)✕0.5+120=124 |
| 6日 | 135円 | (135−124)✕0.5+124=129.5 |
これでEMAの計算が完了です。
なぜEMAの計算式はこんなにややこしいのか?

なんだかややこしいな…

うん、まあちょっと難しいかもしれんの
なぜEMAはこのようなややこしい計算を行うのか?について解説しておきます。
そもそもSMA(単純移動平均線)は期間「n」の平均値です。例えば期間「10」のSMAは10日間の終値の平均値です。
SMAは時間経過すると、新しい日の終値を加える代わりに、最も古い日の終値を削除します。さらにSMAはすべての価格データを(10日前のデータも直近のデータも)平等に取り扱います。その結果、直近の移動平均線の動きに古い(過ぎ去った)価格データが少なからず影響を与えることになり、直近の価格変動が移動平均線に反映されるまでにタイムラグが生じることになるのです。これが単純移動平均線(SMA)の特徴であり弱点でもあります。
SMAの弱点を克服したEMA
SMAの弱点を補うべく考案されたのがEMA(指数平滑移動平均線)です。10日前の価格データと1日前の価格データをフラットに取り扱うのではなく、直近の価格データをより重視し、その一方で古い価格データの比重を軽くします。
その結果、直近の価格変動が移動平均線に反映されるまでのタイムラグが小さくなります。より精度の高い予測が可能になるわけです。
指数関数的減衰とは?
では、どうすれば直近の価格データを重視することができるのか?
その方法とは、新しい価格データから古い価格データへと指数関数的(=exponential)に加重を減衰させていくというもの。
指数関数的減衰とは、ある量が減少する速さが減少する量に比例することを意味します。
ちょっとわかりにくいですが、例えばその逆の「指数関数的増加」は、最近良く耳にしますよね。そうです「コロナウィルスの感染者数」です。コロナウィルス感染者が増加する速さが増加する量に比例することを「感染者数の指数関数的増加」と表します。1倍→2倍→4倍→8倍→16倍…つまり「ねずみ算」のようなイメージです。
指数関数的減衰は、その逆と考えるとわかりやすいのではないでしょうか。減少する量が減るほど減少する速さが減速します。パンデミックの逆ですね。
最新の価格データに大きなウェイトを置き、過去にさかのぼるにつれて小さなウェイトをかけて計算します。その結果、データは指数関数的に減少していきます。この時系列分析手法を指数平滑法と呼びます。
ここまで理解できたら、もう一度下の式をご覧ください。
この式が意味するところは、前回の終値(実績値)と前日EMA(前回予測値)を比較してどれくらい差異があるかを算出し、それに平滑定数を掛けた「修正値」を、前日EMA(前回予測値)に加減してEMA(今回予測値)を計算しているということ。
あくまでも終値(実績値)は「修正値」の算出に使われるのみで、今回の予測値(EMA)のベースになるのは前日EMA(前回予測値)である点が重要です。その結果、直近終値が異常値だったとしても今回のEMAに影響が出すぎないようにしているのです。
平滑化定数は、過去の価格データへの影響度を決定します。0より大きく1より小さいのですが、平滑化定数が1に近いほど直近の価格データを重視し、0に近いほど直近の価格への比重が軽くなります。
平滑化定数の計算式
- 期間10 → 平滑化定数は0.18
- 期間20 → 平滑化定数は0.095
上の例でいえば、期間10の平滑定数(0.18)の方が1により近いため、直近の価格データを重視する結果を吐き出します。
指数平滑移動平均線(EMA)の計算方法|まとめ
指数平滑移動平均線(EMA)の計算方法をなるべく噛み砕いて解説してみました。
計算式さえ理解すれば、手計算することも可能なので、それほど難解ではないと思います。
移動平均線|関連記事
- 移動平均線の期間、最強設定(おすすめ)はこれだ!
- 移動平均線の最適な「組み合わせ」が分からなくなった時…
- 移動平均線|短期・中期・長期の期間設定|最適解はこれだ!
- 移動平均線、5分足スキャルピングに適した期間はどれ?
- 正直、移動平均線だけで勝てるだろ
- ”おまいら200MA(移動平均線)を入れてみろ!勝率がグンッと上がるぞ!”
- 中学生でも理解できる!指数平滑移動平均線(EMA)の計算方法を解説するよ!
- 説明しよう。指数平滑移動平均線(EMA)とはなにか…
- 教えて!グランビルの法則の移動平均線は何日が正しいの?
- 移動平均線の種類、「これだけは覚えとけ」って話。
- 移動平均線の使い方をどこよりもわかりやすく解説するよ!
- たった3本の移動平均線だけでも勝てるって知ってた?
- なぜEMA(指数平滑移動平均線)が最強なのか?
- EMAだけで勝てるって…ウソだろ?
- ねえ、まだ『移動平均線乖離率』を使ってないの?
- 乖離トレードを極める|乖離率とダイバージェンス
- 移動平均線、5分足スキャルピングに適した期間はどれ?
- 200MA(移動平均線)の汎用性の高さにそろそろ気付くべき!
- 200MAだけで6年間負け無し!『883手法』を紹介するよ!
- 期間の異なる複数の移動平均線のトレンドを視覚的に把握できるインジケーターを紹介するよ!
- Alex5757000_Multi_Moving_Average.mq4はあくまでも環境認識用ツールとして活用するべき
- 移動平均線(MA)の傾き(角度)を測るインジケーターを紹介するよ!
- 移動平均線の傾き(角度)でトレードする方法を考察するよ!
- 移動平均線の傾き(角度)を数値化して仕掛けと手仕舞いを考えてみたよ!
- 移動平均の傾きでトレーリングストップする方法を考察するよ!
- 【スキャルピング】移動平均線を1分足で使うのはアリか?
- 5分足移動平均線でスキャル、たったこれだけで勝てるよ!
- TMA(三角移動平均線)…なにそれ?おいしいの?
- TMA(三角移動平均線)の計算式、小学生レベルの算数で解き明かすよ!
- 三角移動平均線、2回SMA化したら中央値の比重が高まるのはなぜか?
- 【勝てる!】EMAクロスをRSIとストキャスでフィルタリングしたシンプルFX手法!
- パラボリックSARのパーフェクトオーダーと移動平均線のパーフェクトオーダーの違いについて解説するよ!
- パラボリックSARに200移動平均線(EMA)を引いてみろ、優位性が高まるぞ!
- 5本のEMAが収束して一気に拡散、MAビッグバンを狙え!
- 平均足同時線と移動平均線を組み合わせたストラテジーを考察してみる
- パーフェクトオーダーの「押し目買い・戻り売り」で仕掛ける方法を紹介するよ!