TMA(三角移動平均線)の計算式を紐解く
前回の記事TMA(三角移動平均線)…なにそれ?おいしいの?にて、TMAの計算式は以下の通りであると解説しました。
TMAの計算式
- TMA=SMA(SMA)
つまり、TMAは単純移動平均線(SMA)をもう一度移動平均(SMA)化したもであると。実際のところ海外の投資サイトでは以下のように紹介されることが大半です。
海外サイトでよく見かけるTMAの計算式
- SMA=(P1 + P2 + P3 + P4 + … + Pn)/ n
- TMA=(SMA1 + SMA2 + SMA3 + SMA4 + … SMAn)/ n
その一方で、
余談ですが、日本のWEBサイトでは、TMAは中央の値に加重をかけて計算する…と解説されているものもありますね。いわば加重移動平均線の一種です。以前紹介したLWMA(線形加重移動平均線)も同じように加重を考慮した移動平均線でした(LWMAは直近のローソク足の重み(n=Weight)が最大であり、そこから過去に遡るごとに、徐々に比重を線形(=Liner)に減らしていきます。最終的な比重は1になります。)。一方のTMA(三角移動平均線)は、中央値に加重を加えて移動平均化していると解説されているサイトを見かけます。この中央値に加重をかけたTMAについては、出処がよくわかりません。海外ではメジャーではないように感じます。海外のWEBサイトでは、シンプルにSMAを再SMA化したものがTMAである…という解説が一般的だからです。
とお伝えしました。
つまり、TMA(三角移動平均線)について、日本と海外とでは異なる解釈がされているのでは?という素朴な疑問です。
TMA(三角移動平均線)の計算式について勘違いをしていた…
気になって海外サイトを漁って詳しく調べてみました。
すると…!
The Triangular Moving Average (TRIMA) represents an average of prices, but places weight on the middle prices of the time period. The calculations double-smooth the data using a window width that is one-half the length of the series.
”but places weight on the middle prices of the time period.”つまり、期間の中間価格にウェイトを置く…とあります。
さらに、The calculations double-smooth the data using a window width that is one-half the length of the series.…系列の長さの半分のウィンドウ幅を使用してデータを二重に平滑化して計算する…と記載されています。
なるほど!ようやく意味がわかりました。私が勘違いしていました。
改めてTriangularMA.mq4やtma centered.mq4などの海外インジケーターの中身(MQLソースコード)を詳しく調べ、やっと理解できました。
そして、各インジケーターのプロパティにおいて期間(period)ではなく、Half Length(=半分の長さ)が使われている意味もわかりました。
TMA(三角移動平均線)の計算モデルはTMA=SMA(SMA)で正しいのですが、詳しくは以下の通りです。
TriS-MA = SUM(MA1,L) / L
Where:
MA1 = SUM(CLOSE,L) / L
L = ceiling((n+1) / 2)
n = Number of Periods引用:http://etfhq.com/blog/tag/triangular-moving-average/
上の式を紐解きます。
まず、最初にSMA化(=L期間の終値を合計してL期間で割る)しますが、そのときに使用する期間は「L=(TMAの期間+1)÷2」です。ここで算出したSMAがMA1です。さらに「L=(TMAの期間+1)÷2」期間分のMA1を合計したうえで、L期間で割ってSMA化します(2回目)。その結果がTMAとなります。
ちょっとわかりにくいので簡略化してみます。

Triangular Moving Average
TMAを算出する際の、計算式におけるSMA期間は、TMAの期間とは異なるのですね。
なんだか複雑になってしまいましたが、上の計算式、実は期間の中央値に比重(ウエイト)を置いて計算する方法を簡略化したものだったのです。
【2026年1月版】優位性の高いFX商材 Best4
期間の中央値に比重を置いて計算するとはどういう意味か?
まず期間の中央値に比重(ウエイト)を置くという意味を理解する必要があります。例えば5日間のTMAを算出する場合、以下のように比重バランスをおこないます。
比重バランス
- 1日目…比重1
- 2日目…比重2
- 3日目…比重3(中央値が最もウエイトが大きい)
- 4日目…比重2
- 5日目…比重1
仮にレートが以下の通りだった場合…
- 1日目…101円
- 2日目…102円
- 3日目…103円
- 4日目…104円
- 5日目…105円
TMAはそれぞれの価格に比重を掛けて足したものを、”比重の合計”で割って算出します。
TMA計算式
- TMA =(101✕1+102✕2+103✕3+104✕2+105✕1)÷(1+2+3+2+1)
=(101+204+309+208+105)÷9
= 927÷9
= 103
この計算方法は中央値の比重が最も高く、両サイド(最古のデータ&最新のデータ)に行くに従って比重が下がります。図にすると以下の通り。
TMAの概念
比重の形が中央を頂点とする二等辺三角形になりますね。だからトライアングル(Tryangle)なんですね。
- TMA=Triangle Moving Average(トライアングルMA)
ここまで理解できたところで、実際の計算式をもう一度ご覧ください。

Triangular Moving Average
上の計算式のどこがどのように三角形なのでしょうか?まったくわかりませんよね。先に述べたように、上の計算式は中央値に比重をかける計算式を単純化したもです。
実際に計算してみるとわかります。
TMA(三角移動平均線)を計算してみよう!
上で解説した計算式を使ってTMAを計算してみます。

Triangular Moving Average
例えば期間5のTMAを算出するためには、まずSMAを算出しますがそのためのSMA期間は次の通り。
SMA算出期間
- SMAの算出期間=(5+1)÷2=3
つまり期間3のSMAを最初に算出します。
仮に以下のようなレートがあったとします。
- 1日目:102円
- 2日目:101円
- 3日目:103円
- 4日目:102円
- 5日目:105円
- 6日目:102円
- 7日目:101円
- 8日目:103円
- 9日目:102円
- 10日目:104円
- 11日目:102円
- 12日目:103円
- 13日目:104円
- 14日目:106円
- 15日目:107円
- 16日目:105円
- 17日目:103円
- 18日目:102円
- 19日目:101円
- 20日目:99円
まず最初に3日間の単純移動平均線(SMA)を計算してみましょう。計算できるのは3日目からですね。
- 1日目:99円
- 2日目:100円
- 3日目:101円 SMA=(99+100+101)÷3=100.00円
- 4日目:102円 SMA=(100+101+102)÷3=101.00円
- 5日目:105円 SMA=(101+102+105)÷3=102.67円
- 6日目:102円 SMA=(102+105+102)÷3=103.00円
- 7日目:101円 SMA=(105+102+101)÷3=102.67円
- 8日目:103円 SMA=(102+101+103)÷3=102.00円
- 9日目:102円 SMA=(101+103+102)÷3=102.00円
- 10日目:104円 SMA=(103+102+104)÷3=103.00円
- 11日目:102円 SMA=(102+104+102)÷3=102.67円
- 12日目:103円 SMA=(104+102+103)÷3=103.00円
- 13日目:104円 SMA=(102+103+104)÷3=103.00円
- 14日目:106円 SMA=(103+104+106)÷3=104.33円
- 15日目:107円 SMA=(104+106+107)÷3=105.67円
- 16日目:105円 SMA=(106+107+105)÷3=106.00円
- 17日目:103円 SMA=(107+105+103)÷3=105.00円
- 18日目:102円 SMA=(105+103+102)÷3=103.33円
- 19日目:101円 SMA=(103+102+101)÷3=102.00円
- 20日目:99円 SMA=(102+101+99)÷3=100.67円
次に、先ほど算出したSMAをさらに期間3日でSMAを算出します。これが期間5のTMA(三角移動平均線)になります。
- 3日目SMA:100.00円
- 4日目SMA:101.00円
- 5日目SMA:102.67円 TMA=(100.00+101.00+102.67)÷3=101.22円
- 6日目SMA:103.00円 TMA=(101.00+102.67+103.00)÷3=102.22円
- 7日目SMA:102.67円 TMA=(102.67+103.00+102.2)÷3=102.78円
- 8日目SMA:102.00円 TMA=(103.00+102.2+102.00)÷3=102.56円
- 9日目SMA:102.00円 TMA=(102.2+102.00+102.00)÷3=102.22円
- 10日目SMA:103.00円 TMA=(102.00+102.00+103.00)÷3=102.33円
- 11日目SMA:102.67円 TMA=(102.00+103.00+102.67)÷3=102.56円
- 12日目SMA:103.00円 TMA=(103.00+102.67+103.00)÷3=102.89円
- 13日目SMA:103.00円 TMA=(102.67+103.00+103.00)÷3=102.89円
- 14日目SMA:104.33円 TMA=(103.00+103.00+104.33)÷3=103.44円
- 15日目SMA=105.67円 TMA=(103.00+104.33+105.67)÷3=104.33円
- 16日目SMA:106.00円 TMA=(104.33+105.67+106.00)÷3=105.33円
- 17日目SMA:105.00円 TMA=(105.67+106.00+105.00)÷3=105.56円
- 18日目SMA:103.33円 TMA=(106.00+105.00+103.33)÷3=104.78円
- 19日目SMA=102.00円 TMA=(105.00+103.33+102.00)÷3=103.44円
- 20日目SMA=100.67円 TMA=(103.33+102.00+100.67)÷3=102.00円
SMAを期間3で「2回」計算することで、期間5のTMAを算出することができました。
では、ここから別の計算方法でTMA(期間5)を算出します。中央値に比重を置く計算方法です。
- 1日目…比重1
- 2日目…比重2
- 3日目…比重3(中央値が最もウエイトが大きい)
- 4日目…比重2
- 5日目…比重1
計算式は以下の通り。
TMA =(1日目価格✕1+2日目価格✕2+3日目価格✕3+4日目価格✕2+5日目価格✕1)÷(1+2+3+2+1)
- 1日目:102円
- 2日目:101円
- 3日目:103円
- 4日目:102円
- 5日目:105円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=101.22円
- 6日目:102円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102,22円
- 7日目:101円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.78円
- 8日目:103円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.56円
- 9日目:102円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.22円
- 10日目:104円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.33円
- 11日目:102円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.56円
- 12日目:103円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.89円
- 13日目:104円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.89円
- 14日目:106円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=103.44円
- 15日目:107円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=104.33円
- 16日目:105円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=105.33円
- 17日目:103円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=105.56円
- 18日目:102円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=104.78円
- 19日目:101円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=103.44円
- 20日目:99円 TMA=(102✕1+101✕2+103✕3+102✕2+105✕1)÷9=102.00円
ご覧の通り、2回SMA化した結果と全く同じになりましたね。Excelで試算してみるとよくわかります。
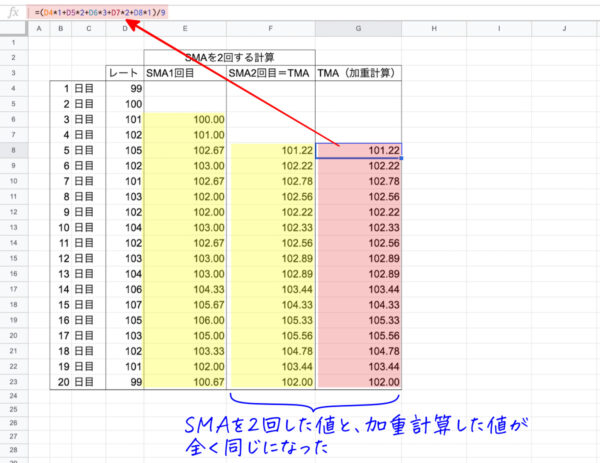
TMA(三角移動平均線)の計算
どちらの計算方法でも全く同じ値を返すことがわかりましたね。つまり…どちらでもOKってことです。
中央に比重をかけた計算式でも、SMAを2回おこなう計算式でも同じ結果になります。
ただ、日本のWEBサイトでここまで詳しく解説しているページは、残念ながらほとんど見つかりませんでした。
ただたんに、「単純移動平均線(SMA)化を2回おこなって計算する…」とか、「中央値に比重をかけて計算する…」など、どうも説明が足りていません。
単純移動平均線(SMA)化を2回行うならば、その期間は「(TMA期間n+1)÷2」とするのが正解です。
これでスッキリしましたね。







