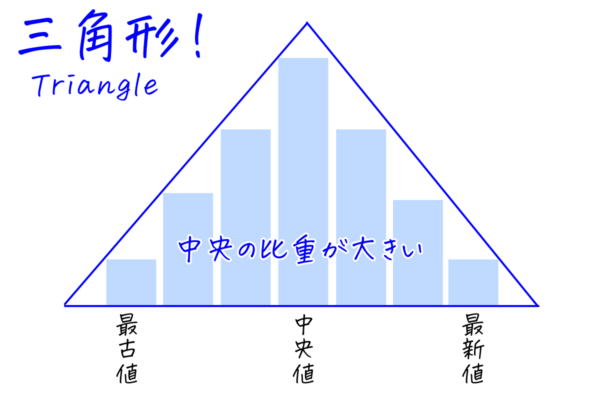
三角移動平均線(TMA)、2回SMA化したら中央値の比重が高まるのはなぜか?
前回の記事TMA(三角移動平均線)の計算式、小学生レベルの算数で解き明かすよ!にご質問をいただきました。
SMA化を2回することで三角移動平均線を算出するのはわかったが、なぜ2回SMA化すると中央値の比重が高まるのか?
…という内容です。
たしかに説明が不十分だったかもしれません。まず三角移動平均線(TMA=Triangle Moving Average)の概念についておさらいします。
TMAは、集計するレートの中央値(たとえば5日分であれば3日目)に最も比重をかけて算出します。その中央値から離れるほど比重を軽くするため、比重のバランスが二等辺三角形のような形になります。
これがTMA(三角移動平均線)の概念でしたね。
そして、中央値に比重をかけて計算する方法は以下の通りでした。
期間の中央値に比重を置いて計算するとはどういう意味か?
まず期間の中央値に比重(ウエイト)を置くという意味を理解する必要があります。例えば5日間のTMAを算出する場合、以下のように比重バランスをおこないます。
- 1日目…比重1
- 2日目…比重2
- 3日目…比重3(中央値が最もウエイトが大きい)
- 4日目…比重2
- 5日目…比重1
仮にレートが以下の通りだった場合…
- 1日目…101円
- 2日目…102円
- 3日目…103円
- 4日目…104円
- 5日目…105円
TMAはそれぞれの価格に比重を掛けて足したものを、”比重の合計”で割って算出します。
TMA =(101✕1+102✕2+103✕3+104✕2+105✕1)÷(1+2+3+2+1)
=(101+204+309+208+105)÷9
= 927÷9
= 103
【2026年1月版】優位性の高いFX商材 Best4
かんたんな分数で理解できるよ!
ここで最初の質問に戻ります。
SMA化を2回することで三角移動平均線を算出するのはわかったが、なぜ2回SMA化すると中央値の比重が高まるのか?
どうして2回SMA化すると、中央値の比重がたかまるのでしょうか?詳しく解説します。

Triangular Moving Average
上の計算式は、先に引用した面倒な計算式(比重を考慮しながら集計する計算式)を簡略化したものでしたね。
引用で用いたサンプルをさらに簡略化します。仮にレートが以下の通りだった場合…
- 今日…a円
- 1日前…b円
- 2日前…c円
- 3日前…d円
- 4日前…e円
上の5日分(期間5)のTMA(三角移動平均線)を算出してみましょう。
まず1回目のSMA化ですが、そのときの期間は、(期間n+1)÷2 でしたね。つまり(5+1)÷2=3…期間3でSMA化します。
※ちなみに、(期間n+1)÷2 が小数点を含む場合は、四捨五入して整数に修正します。たとえば期間nが10の場合、(10+1)÷2=5.5 となりますが、四捨五入して「6」として計算します。
期間3のSMAは以下の通りです。
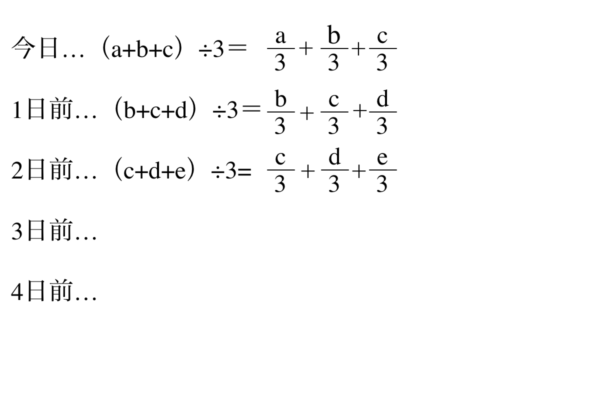
TMA(三角移動平均線)の計算式|その1
ここまでが1回目のSMA化です。次にもう一度SMA化します。期間は同じく「3」です。
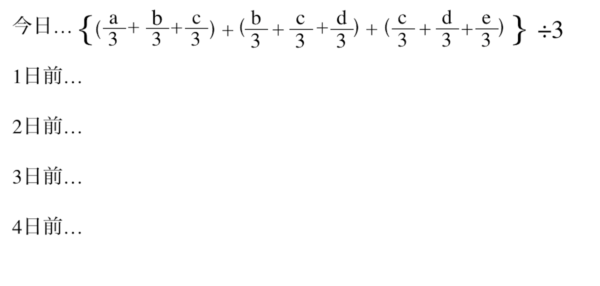
TMA(三角移動平均線)の計算式|その2
「今日」の数式をまとめると以下のようになりますね。
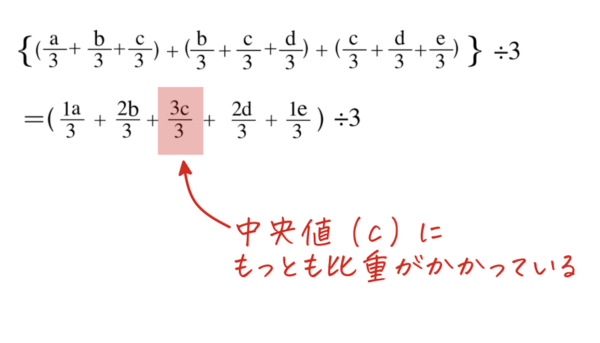
TMA(三角移動平均線)の計算式|その3
ご覧の通り、中央値(2日前のc円)に最も比重(3倍)がかかっていることが理解できます。
そして、中央値から乖離するほど比重が漸減しています。b円とd円には2倍、a円とe円はそれぞれ1倍の比重となっていますね。
- 今日…a円(比重:1)
- 1日前…b円(比重:2)
- 2日前…c円(比重:3)←中央値にもっとも比重がかかっている
- 3日前…d円(比重:2)
- 4日前…e円(比重:1)
以上の説明で、「(期間n+1)÷2」にてSMAを2回行うと中央値の比重が高まることが理解できたと思います。簡単な分数と算数ですね。