ボリンジャーバンド|計算式|よく見かける数式
ボリンジャーバンドは移動平均線からのレートの散らばり具合を上下2本ラインでプロットした指標です。この散らばり具合を算出するのが標準偏差と呼ばれる指標。
今回は、難解とされるボリンジャーバンドの計算方法を、できるだけ文系トレーダーでも理解できるように紐解いて解説していきますね。
まず、「ボリンジャーバンド 計算式」と検索して出てくるサイトでよく見かける計算式がこちら。
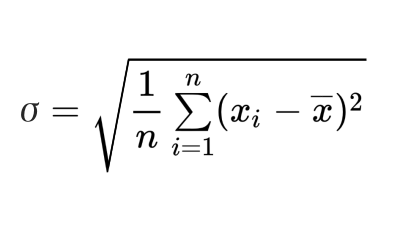
ボリンジャーバンド|計算方法|標準偏差
上の複雑な計算式は標準偏差を求める式(=定義)です。

なんですか?これ?
意味が全くわからないんだけど…

統計学やデータ分析をかじった人間じゃないと、チンプンカンプンじゃろう。
この複雑な式を掲載して「ボリバンの計算式はこれ!」と、サラッと解説を終了しているサイトが非常に多いですよね。
実はこんな難解な計算式を使わずとも容易にボリンジャーバンドの値を算出することは可能です。
この記事を読めば、あなたも簡単に計算できるようになるし、表計算ソフト(エクセルやスプレッドシート)を使ってボリンジャーバンドをものの数分で描写できるようになります。

この記事を読めば、あなたも簡単に計算できるようになるぞ!
また、表計算ソフト(Excel)を使ってボリンジャーバンドを「ものの数分」でグラフ化できるようになれるぞ!
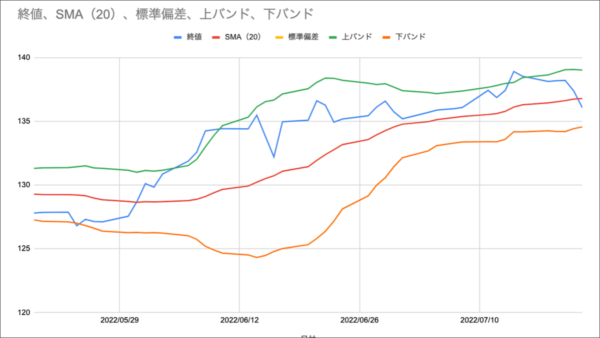
ボリンジャーバンド|計算式|エクセルでグラフ化
上のようなグラフ(ボリンジャーバンド)をExcelで描くところまで、詳しく解説しますね。
ボリンジャーバンド|計算式|標準偏差の基本
まずはボリンジャーバンドの肝(きも)とも言える標準偏差について理解を深めておきましょう。
※かなり噛み砕いているので、細かな部分へのツッコミはなしでお願いしますね。
標準偏差とは?
標準偏差はデータの集合体に含まれるばらつきの平均値です。それぞれの値が平均値からどの程度離れているか(散らばっているか)を表しています。
標準偏差が高いということは、値が全体的に平均値から離れていることを意味します。標準偏差が低いということは、値が平均値に近いところに集まっていることを意味します。
標準偏差でわかること
標準偏差は、正規分布の広がりを示す指標として有効です。
正規分布ではデータは対称に分布し、ほとんどの値は中心付近に集まります。中心から離れるにしたがって値は先細りになります。こんな図を見たことありますよね。
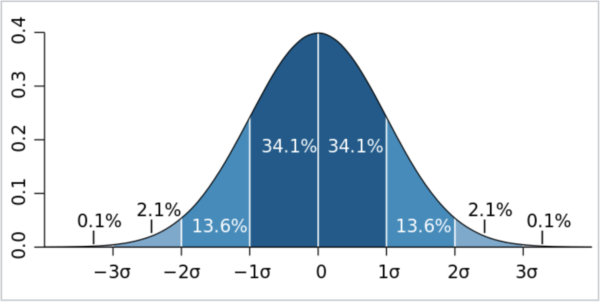
正規分布|出典:Wikipedia
標準偏差はデータが分布の中心からどれくらい離れているかを示します。
たとえば学校のテストの点数や、クラスの身長など、データのバラつき具合を把握したいときに活用されます。
標準偏差と偏差値
最も馴染みがあるのはテストの点数から算出する「偏差値」ですよね。
偏差値は、テストを受けた集団の中での自分の位置を把握するために使われます。
数学で80点を取ったから良いとか悪いとかではなく、同じテストを受けた集団の中において自身の成績がどの程度のポジションにいるのかを、偏差値によって把握することができます。
例えば、平均点が60点の数学のテストであなたが80点を取ったとします。偏差値を計算してみましょう。標準偏差が20の場合です。
偏差値=(80ー60)÷20✕10+50=60
あなたの偏差値は「60」です。
ちなみに偏差値の計算は以下の通り。
仮にあなたが90点を取った場合は?
偏差値=(90ー60)÷20✕10+50=65
あなたの偏差値は「65」です。
偏差値は平均との差を標準偏差で割り、10を掛けて50を足します。標準偏差で割る理由は全体の点数の散らばり具合と自分の点数の差を確認するため。さらに50を足すのは50を基準にして0〜100の間で数値を示すためです。
気になるのは「標準偏差=20」ですよね。
この標準偏差を算出する方法が先の計算式なのですが、ここではあえて手計算してみます。
標準偏差を手動で計算してみる
6人の数学のテスト結果から標準偏差を算出します。まずはデータ(テスト結果)を用意します。
Aさん…65点
Bくん…80点
Cくん…75点
Dさん…85点
Eくん…90点
Fさん…45点
6人の平均値を求めます。
平均値=(65+75+90+85+60+45)÷6=70点
各点数の平均値から偏差(平均値からの乖離)を求めます。
65点…平均値からの乖離(65−70=−5)
75点…平均値からの乖離(75−70=+5)
90点…平均値からの乖離(90−70=+20)
85点…平均値からの乖離(85−70=+15)
60点…平均値からの乖離(60−70=−10)
45点…平均値からの乖離(45−70=−25)
平均値からの偏差をそれぞれ二乗します。この結果「正数」になります。
(-5)2=−5×−5=25
(+5)2=5×5=25
(+20)2=20×20=400
(+15)2=15×15=225
(-10)2=−10×−10=100
(-25)2=−25×−25=625
二乗した偏差をすべて足します。
25+25+400+225+100+625=1400
分散(データのばらつき)を求めるために、データの総数「6」で割ります。
1400÷6=233.33…
分散の「正の平方根」を求めます。ようやく標準偏差が計算できました。
√233.3≒15.27
標準偏差は15.27点です。
この手計算を数式で表したものが以下の計算式なのですね。
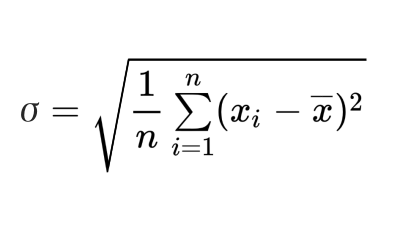
ボリンジャーバンド|計算方法|標準偏差
標準偏差が「15.27点」が意味するところは、平均点の「70点」に対して±15.27点の範囲で点数をとっている人が多いということです。
ではこの数学テストで「90点」を取ったC君の「偏差値」を計算してみます。

テストの点数は90点。
標準偏差は15.27。
全体の平均点は70点。
偏差値=(自分の得点ー平均点)÷標準偏差×10+50
偏差値=(90−70)÷15.27×10+50=63.09…
偏差値=63.1
C君の偏差値は「63.1」です。
ここまでで、標準偏差の意味がなんとなくでも理解できればOKです。
【2026年1月版】優位性の高いFX商材 Best4
ボリンジャーバンド|計算式|具体的な手順
ここからは、先の標準偏差計算方法をボリンジャーバンドの概念に当てはめながら考えていきます。
とりあえず難しい数式は置いておき、手動で計算してみましょう。
計算をシンプルにするために、終値は3つだけ用意します。
終値1…20
終値2…25
終値3…21
まずは中心線である単純移動平均線(SMA)を算出します。
単純移動平均線の計算方法は極めてシンプルです。n本分の単純移動平均線は以下の数式で計算できます。
今回は3つの終値を使いますので、終値を合計して3で割ります。
SMA=(20+25+21)÷3=22
次に標準偏差を求めます。
まずは、各終値の「平均値から偏差(平均値からの乖離)」を求めます。平均値は「22」でしたね。
終値20…平均値からの乖離(20−22=-2)
終値25…平均値からの乖離(25−22=+3)
終値21…平均値からの乖離(21−22=-1)
平均値からの偏差をそれぞれ二乗します。この結果「正数」になります。
(−2)2=-2×-2=4
(+3)2=3×3=9
(−1)2=-1×-1=1
二乗した偏差をすべて足します。
4+9+1=14
分散(データのばらつき)を求めるために、データの総数「3」で割ります。
14÷3=4.66…
分散の「正の平方根」を求めます。ようやく標準偏差が計算できました。
√4.66≒2.15
標準偏差は2.15です。
この標準偏差を使って上下のバンドを計算するには以下の式を使用します。
- 上バンド…SMA+(標準偏差✕2)
- 下バンド…SMA−(標準偏差✕2)
実際に計算してみましょう。
上バンド=SMA+(標準偏差✕2)
上バンド=22+(2.15✕2)
上バンド=26.3
下バンド=SMA−(標準偏差✕2)
下バンド=22−(2.15✕2)
下バンド=17.7
これで3つの数値(センター、上バンド、下バンド)が出揃いました。
- 上バンド(+2σ)…26.3
- センターライン(SMA)…22
- 下バンド(−2σ)…17.7
あとはこれを繰り返し計算するだけです。
ロジックさえわかっていれば手動で計算することも容易です。
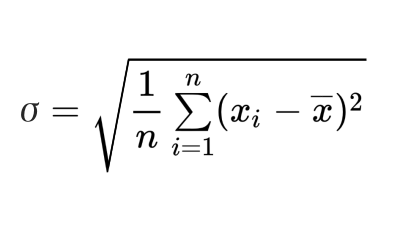
ボリンジャーバンド|計算方法|標準偏差
上のような難しい数式を使わずとも手動でも計算できますね。
【2026年1月版】優位性の高いFX商材 Best4
ボリンジャーバンド|計算式|Excel(エクセル)
上の解説が理解できれば、表計算ソフトのExcel(エクセル)を使って簡単に算出することが可能です。※Googleスプレッドシートでも全く同じ計算ができます。
まずはUSD/JPY(ドル円)の終値を用意します。
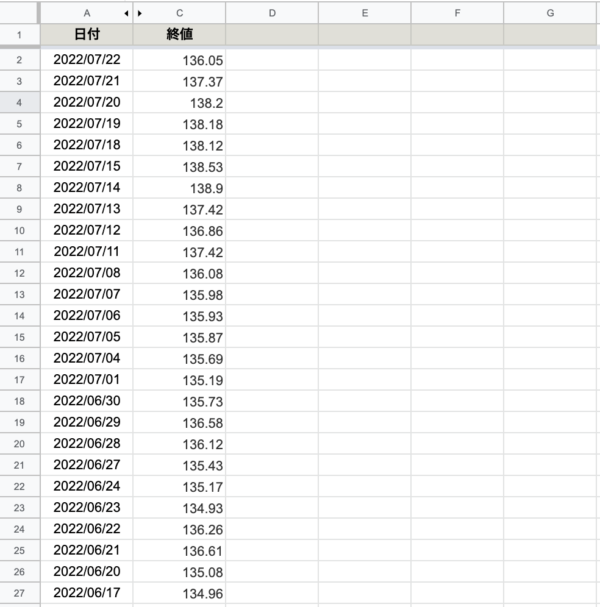
ボリンジャーバンド|計算式|エクセル|終値を用意
次にSMA(期間20)、標準偏差、上バンド、下バンドを算出する列を作ります。
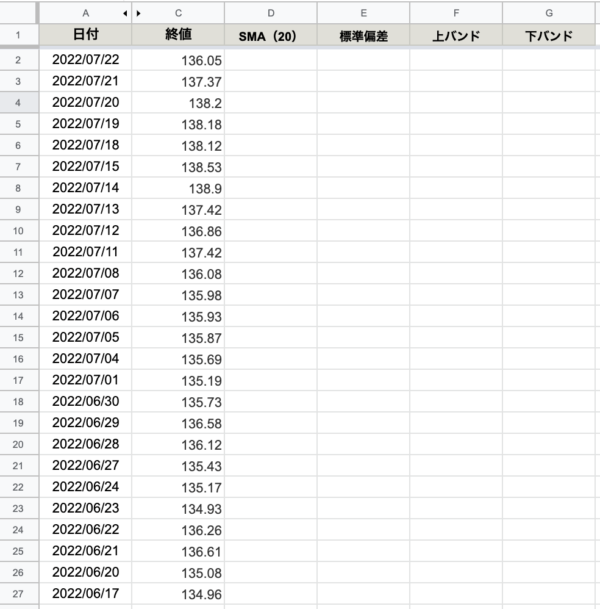
ボリンジャーバンド|計算式|エクセル|列を作る
項目行を除く一番上の行(2行目)のセルに数式を入れます。
SMA(セルD2)は単純に上から20個の終値を合計して20で割るだけ。
=AVERAGE(C2:C21)
標準偏差(セルE2)はエクセルやスプレッドシートに備わっているSTDEV.P関数を使います。STDEV.P関数でデータ範囲、つまり終値を20個選択してあげれば自動的に計算してくれます。
=STDEV.P(C2:C21)
もちろん手計算でも可能ですが、ここはシンプルに関数を使ったほうが早いです。
上バンド(セルF2)と下バンド(セルG2)は、SMA(単純移動平均線)に先ほど計算した標準偏差をプラス・マイナスする式を入力します。偏差「2」で計算する場合は以下の通り。
=D2+(E2*2)
=D2–(E2*2)
それぞれのセルに数式を入力します。
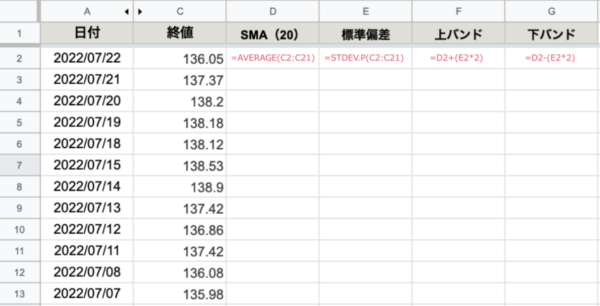
ボリンジャーバンド|計算式|エクセル|セルに計算式を入れる
あとは一気にセルを下までコピペするだけ。2行目を下までドラッグドロップです。
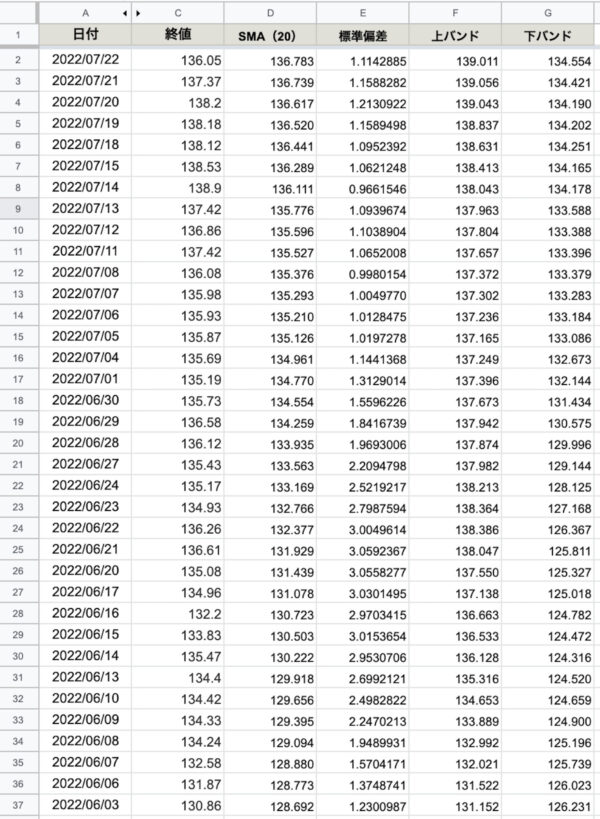
ボリンジャーバンド|計算式|エクセル|セルを下までコピー
Excel(エクセル)で算出した数値でグラフを作成してみましょう。

ボリンジャーバンド|計算式|エクセルでグラフ化
ご覧の通り、ものの数分で期間「20」標準偏差「2」のボリンジャーバンドをExcelで描くことができました。
このグラフを実際のMT4ボリンジャーバンドと比較してみます。
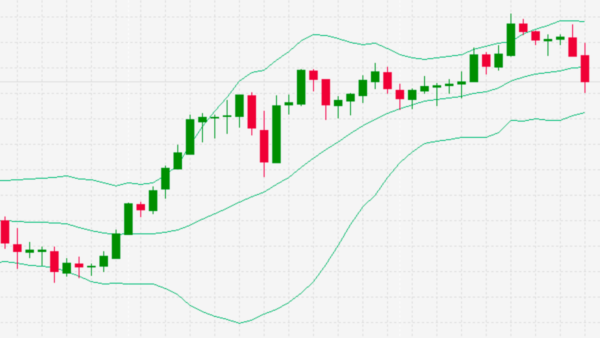
ボリンジャーバンド|計算式|MT4と比較
もっとわかりやすくするためにラインチャートにしてみましょう。

ボリンジャーバンド|計算式|エクセルでグラフ化
上(↑)がExcel(エクセル)で算出したボリンジャーバンド。
下(↓)が(ローソク足終値をライン化した)MT4のボリンジャーバンドです。
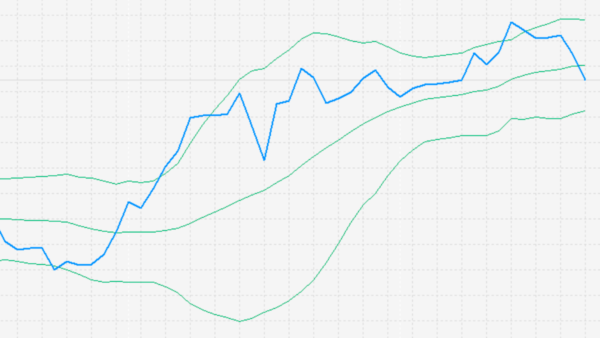
ボリンジャーバンド|計算式|MT4(ラインチャート)と比較
Excel(エクセル)で算出したボリンジャーバンドが、MT4のものと同じ波形を描いていることがわかります。
標準偏差さえ理解できれば意外と簡単ですよね。
ボリンジャーバンド|計算式|まとめ
駆け足でボリンジャーバンドの計算方法を解説しました。標準偏差の概念からスタートし、実際のボリバンの値を手動で計算し、最後に表計算ソフトのExcel(エクセル)で計算した上でMT4と同じようなボリンジャーバンドをグラフ化しました。

なるほど!
かなり噛み砕いて解説してもらったから、すごく理解できたよ!
想像していたより難しくないんだね!

難解とされるボリンジャーバンド計算式も、ここまで分解すれば誰でも理解できるはずじゃよ。







